The identity \(\mathcal{V}\) matrix, \(X \times X \xrightarrow{I_X} \mathcal{V}\) has \(I\) on the diagonal entries and \(0\) on the off-diagonal entries.
A matrix with entries in \(\mathcal{V}\), where \(\mathcal{V}=(V, \leq, \otimes, I)\) is a quantale. (A \(\mathcal{V}\) matrix). Matrix multiplication between \(\mathcal{V}\) matrices
Need two sets, and function \(X \times Y \xrightarrow{M} V\). Call \(M(x,y)\) the (x,y)th entry.
We can multiply \(X \times Y \xrightarrow{M} V\) and \(Y \times Z \xrightarrow{N} V\) to get a new \(\mathcal{V}\) matrix \(X \times Z \xrightarrow{M*N} V\).
\((M*N)(x,z)(x,z)\) defined as \(\bigvee_y\ M(x,y)\otimes N(y,z)\)
Note that this is similar to the standard matrix multiplication, with \(\bigvee \mapsto \Sigma, \otimes \mapsto *\)*
Let \(\mathcal{V}=\mathbf{Bool}\). Here is matrix multiplication \(M*N\) with \(X=\bar{3}, Y=\bar{2},Z=\bar{3},M=X\times Y\rightarrow Z, N=Y\times Z\rightarrow B\).
\(X\)
| F | F |
|---|---|
| F | T |
| T | T |
\(Y\)
| T | T | F |
|---|---|---|
| T | F | T |
\(X*Y\)
| F | F | F |
|---|---|---|
| T | F | T |
| T | T | T |
Write the 2x2 identity matrices for each of the quantales:
\((\mathbb{N},\leq,1,*)\)
\(\mathbf{Bool}:=(\mathbb{B},\leq,true,\land)\)
\(\mathbf{Cost}:=([0,\infty],\leq,0,+)\)
| 1 | 0 |
|---|---|
| 0 | 1 |
| T | F |
|---|---|
| F | T |
| 0 | \(\infty\) | |
|---|---|---|
| \(\infty\) | 0 |
Let \(\mathcal{V}=(V,\leq,I,\otimes,\multimap)\) be a quantale. Prove:
The identity law
For all \(\mathcal{V}\) matrices \(X\times Y\xrightarrow{M}V\), one has \(I_X * M = M\)
The associative law
For any matrices \(W \times X \xrightarrow{M} V, X \times Y \xrightarrow{N} V, Y \times Z \xrightarrow{P} V\), one has \((M*N)*P=M*(N*P)\)
\(\forall v \in \mathcal{V}\), we have \(0 \otimes v \cong 0\).
\(0 \otimes v\)
\(\cong v \otimes 0\) – symmetry
\(= v \otimes \bigvee_{a \in \varnothing} a\) – definition of \(0\)
\(\cong \bigvee_{a \in \varnothing} v \otimes a\) – \(-\otimes x\) preserves joins b/c it is left adjoint
\(= 0\) – definition of 0
Plug this into definition of matrix multiplication
\(I_X * M(x,y)\)
\(= \bigvee_{x'}I_x(x,x')\otimes M(x',y)\) – definition of matrix multiplication in a quantale
\(=(I_x(x,x)\otimes M(x,y))\vee(\bigvee_{x'\ne x}I_x(x,x')\otimes M(x',y))\) – split join into two cases
\(=(I\otimes M(x,y))\vee(\bigvee_{x'\ne x}0\otimes M(x',y))\) – Definition of identity matrix
\(=M(x,y)\vee 0\) – join of a singleton set
\(=M(x,y)\) – Zero is the least element in \(\mathcal{V}\)
Need to show \(\underset{y \in Y}\bigvee (\underset{x\in X}\bigvee M(w,x)\otimes N(x,y))\otimes P(y,z)\) is the same as \(\underset{x \in X}\bigvee M(w,x)\otimes(\underset{y \in Y}\bigvee N(x,y) \otimes P(y,z))\) for all \(w \in W,z \in Z\)
The associativity of \(\otimes\) and the fact it preserves joins b/c it is left adjoint lets us shift the symbols around appropriately.
Consider the distance matrix represented by this graph from Exercise 2.60:
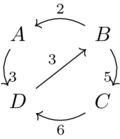
| \(\rightarrow\) | A | B | C | D |
|---|---|---|---|---|
| A | 0 | 6 | 3 | 11 |
| B | 2 | 0 | 5 | 5 |
| C | 5 | 3 | 0 | 8 |
| D | 11 | 9 | 6 | 0 |
Compute the distance matrix by power iteration of the matrix of the presentation.
| \(M\) | A | B | C | D |
|---|---|---|---|---|
| A | 0 | \(\infty\) | \(\infty\) | 3 |
| B | 2 | 0 | 5 | \(\infty\) |
| C | \(\infty\) | \(\infty\) | 0 | 6 |
| D | \(\infty\) | 3 | \(\infty\) | 0 |
| \(M^2\) | A | B | C | D |
|---|---|---|---|---|
| A | 0 | 6 | \(\infty\) | 3 |
| B | 2 | 0 | 5 | 11 |
| C | \(\infty\) | 9 | 0 | 6 |
| D | 5 | 3 | 8 | 0 |
After this, \(M^n\) is the \(\rightarrow\) matrix